Stack

A stack is a collection of objects that are inserted and removed according to the last-in, first-out (LIFO) principle. A user may insert objects into a stack at any time, but may only access or remove the most recently inserted object that remains (at the so-called “top” of the stack).

The name “stack” is derived from the metaphor of a stack of plates in a spring-loaded, cafeteria plate dispenser.

In this case, the fundamental operations involve the “pushing” and “popping” of plates on the stack. When we need a new plate from the dispenser, we “pop” the top plate off the stack, and when we add a plate, we “push” it down on the stack to become the new top plate.

Perhaps an even more amusing example is a PEZ® candy dispenser, which stores mint candies in a spring-loaded container that “pops” out the topmost candy in the stack when the top of the dispenser is lifted.

LIFO Principle of Stack

In programming terms, putting an item on top of the stack is called push and removing an item is called pop.

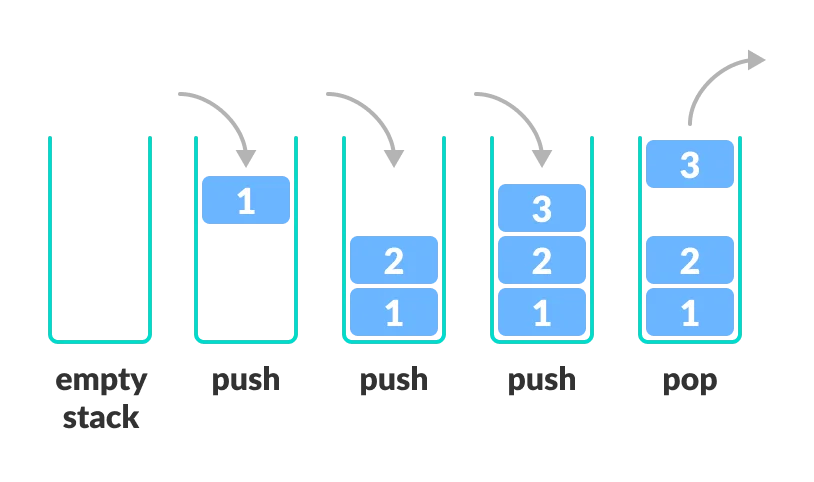
In the above image, although item 3 was kept last, it was removed first. This is exactly how the LIFO (Last In First Out) Principle works.

We can implement a stack in any programming language like C, C++, Java, Python or C#, but the specification is pretty much the same.

Stack Operations

Push #

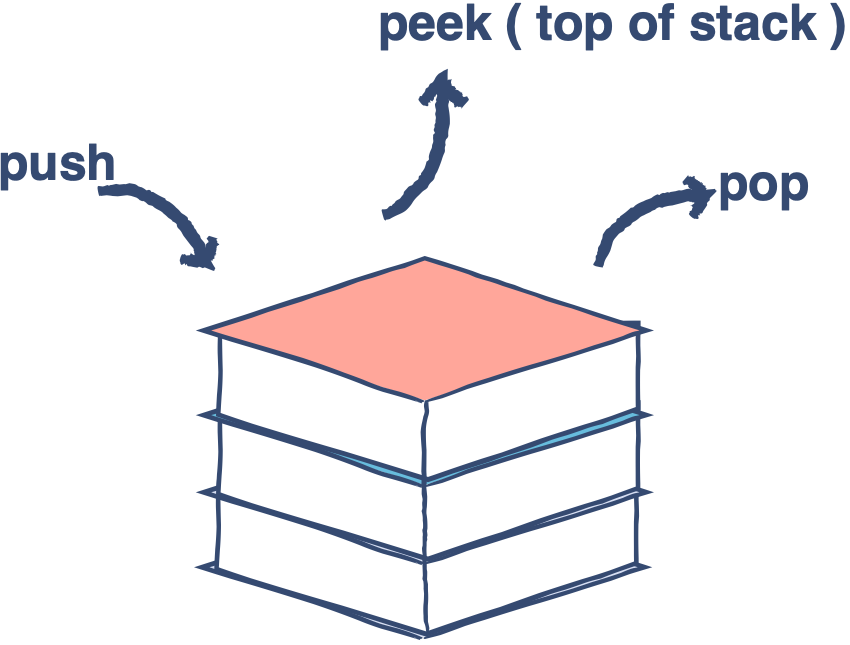
The operation to insert elements in a stack is called push. When we push the book on a stack, we put the book on the previous top element which means that the new book becomes the top element. This is what we mean when we use the push operation, we push elements onto a stack. We insert elements onto a stack and the last element to be pushed is the new top of the stack.

Pop #

There is another operation that we can perform on the stack, popping. Popping is when we take the top book of the stack and put it down. This implies that when we remove an element from the stack, the stack follows the First-In, Last Out property. This means that the top element, the last to be inserted, is removed when we perform the pop operation.

Push and Pop are two fundamental routines that we’ll need for this data structure.

Peek/Top #

Another thing that we can do is view the top element of the stack so we can ask the data structure: “What’s the top element?” and it can give that to us using the peek operation. Note that the peek operation does not remove the top element, it merely returns it.

We can also check whether or not the stack is empty, and a few other things too, that will come along the way as we implement it.

In Python, a stack is implemented using a list object.

To push an item in the stack, use the list function append list.append(item)
To pop an item in the stack, use the list function pop list.pop()
To get the top most item in the stack, write list[-1]

Code:

list=[]

list.append(1) # append 1
print("push:",list)
list.append(2) # append 2
print("push:",list)
list.append(3) # append 3
print("push:",list)

list.pop() # pop 3
print("pop:",list)

print("peek:",list[-1]) # get top most element

list.pop() # pop 2
print("pop:",list)

print("peek:",list[-1]) # get top most element

Exercise:

Try to reverse a list using a stack

#Solution

list=[1,2,3,4,5]
list.append(6)
list.append(7)

print("List before reversal:",list)

for i in range(0,len(list)):
    list.insert(i,list.pop())

print("List after reversal:",list)

Stack Time Complexity

For the array-based implementation of a stack, the push and pop operations take constant time, i.e. O(1).

Applications of Stack Data Structure

Although stack is a simple data structure to implement, it is very powerful. The most common uses of a stack are:

To reverse a word - Put all the letters in a stack and pop them out. Because of the LIFO order of stack, you will get the letters in reverse order.
In compilers - Compilers use the stack to calculate the value of expressions like 2 + 4 / 5 * (7 - 9) by converting the expression to prefix or postfix form.
In browsers - The back button in a browser saves all the URLs you have visited previously in a stack. Each time you visit a new page, it is added on top of the stack. When you press the back button, the current URL is removed from the stack, and the previous URL is accessed.

Queue

Another fundamental data structure is the queue. It is a close “cousin” of the stack, but a queue is a collection of objects that are inserted and removed according to the first-in, first-out (FIFO) principle. That is, elements can be inserted at any time, but only the element that has been in the queue the longest can be next removed.

We usually say that elements enter a queue at the back and are removed from the front. A metaphor for this terminology is a line of people waiting to get on an amusement park ride. People waiting for such a ride enter at the back of the line and get on the ride from the front of the line. There are many other applications of queues.

Stores, theaters, reservation centers, and other similar services typically process customer requests according to the FIFO principle. A queue would therefore be a logical choice for a data structure to handle calls to a customer service center, or a wait-list at a restaurant. FIFO queues are also used by many computing devices, such as a networked printer, or a Web server responding to requests.

There are four different types of queues:

Simple Queue (A normal queue)
Circular Queue
Priority Queue
Double Ended Queue

FIFO Representation of a Queue

In the above image, since 1 was kept in the queue before 2, it is the first to be removed from the queue as well. It follows the FIFO rule.

In programming terms, putting items in the queue is called enqueue, and removing items from the queue is called dequeue.

We can implement the queue in any programming language like C, C++, Java, Python or C#, but the specification is pretty much the same.

Basic Operations of Queue

A queue is an object (an abstract data structure - ADT) that allows the following operations:

Enqueue/put: Add an element to the end of the queue
Dequeue/get: Remove an element from the front of the queue
IsEmpty: Check if the queue is empty
IsFull: Check if the queue is full
Peek: Get the value of the front of the queue without removing it

Working of Queue

Queue operations work as follows:

two pointers FRONT and REAR
FRONT track the first element of the queue
REAR track the last element of the queue
initially, set value of FRONT and REAR to -1

Enqueue Operation

check if the queue is full
for the first element, set the value of FRONT to 0
increase the REAR index by 1
add the new element in the position pointed to by REAR

Dequeue Operation

check if the queue is empty
return the value pointed by FRONT
increase the FRONT index by 1
for the last element, reset the values of FRONT and REAR to -1

Code:

from queue import Queue
  
# Initializing a queue
q = Queue(maxsize = 3)
  
# qsize() give the maxsize 
# of the Queue 
print(q.qsize()) 
  
# Adding of element to queue
q.put('a')
q.put('b')
q.put('c')
  
# Return Boolean for Full 
# Queue 
print("\nFull: ", q.full()) 
  
# Removing element from queue
print("\nElements dequeued from the queue")
print(q.get())
print(q.get())
print(q.get())
  
# Return Boolean for Empty 
# Queue 
print("\nEmpty: ", q.empty())

# The line below would make the program go
# into an infinite loop if the Queue is empty. 
# print(q.get())

q.put(1)
print("\nEmpty: ", q.empty()) 
print("Full: ", q.full())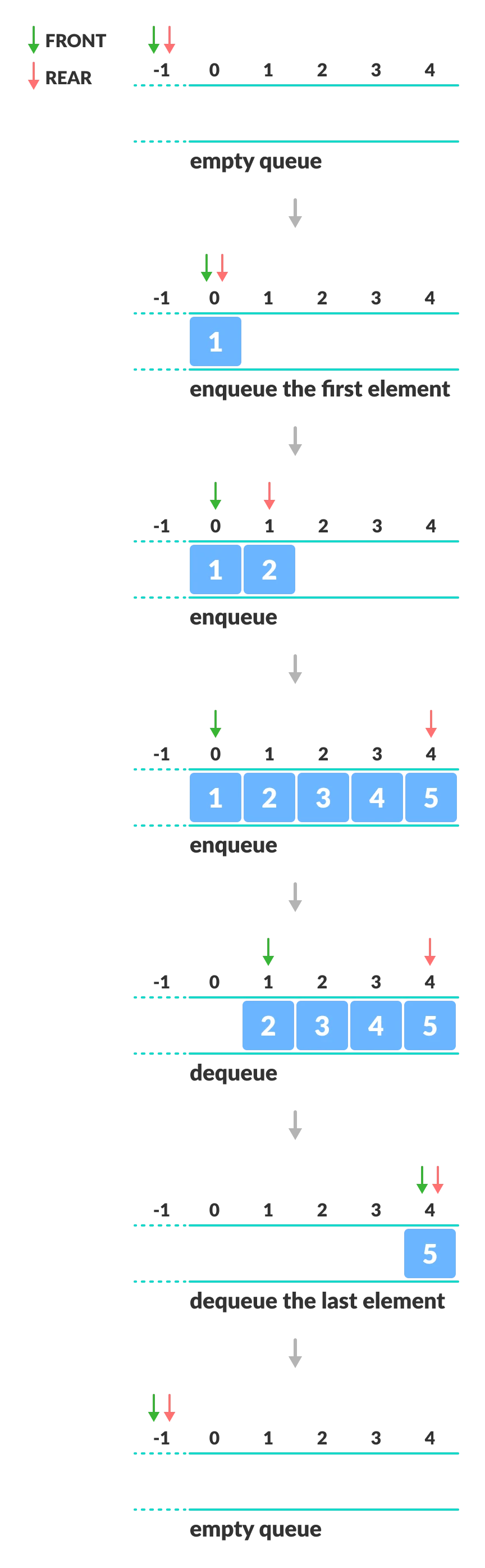

Limitations of Queue

As you can see in the image below, after a bit of enqueuing and dequeuing, the size of the queue has been reduced.

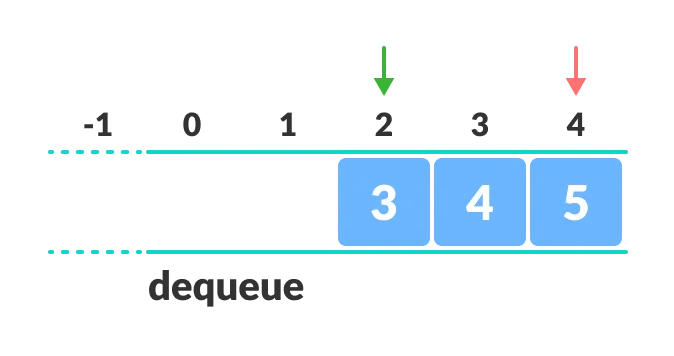
And we can only add indexes 0 and 1 only when the queue is reset (when all the elements have been dequeued).

After REAR reaches the last index, if we can store extra elements in the empty spaces (0 and 1), we can make use of the empty spaces. This is implemented by a modified queue called the circular queue.

Complexity Analysis

The complexity of enqueue and dequeue operations in a queue using an array is O(1). If you use pop(N) in python code, then the complexity might be O(n) depending on the position of the item to be popped.

Applications of Queue

CPU scheduling, Disk Scheduling

When data is transferred asynchronously between two processes.The queue is used for synchronization. For example: IO Buffers, pipes, file IO, etc

Handling of interrupts in real-time systems.

Call Center phone systems use Queues to hold people calling them in order.

Double-Ended Queues (Deques)

Deque or Double Ended Queue is a type of queue in which insertion and removal of elements can either be performed from the front or the rear. Thus, it does not follow FIFO rule (First In First Out).

Types of Deque

Input Restricted Deque
In this deque, input is restricted at a single end but allows deletion at both the ends.

Output Restricted Deque
In this deque, output is restricted at a single end but allows insertion at both the ends.

Illustration

Below is a brief description of the methods used to modify a deque:

Insertion

append(item): Add an item to the right end.

appendleft(item): Add an item to the left end.

insert(index, value): Add an element with the specified value at the given index.

extend(list): This function is used to insert multiple values at the right end. It takes a list of values as an argument.

extendleft(list): This function is similar to extend(), but it reverses the list of values passed as the argument and then appends that list to the left end of the deque.

Deletion

pop(): Remove an element from the right end.

popleft(): Remove an element from the left end.

remove(value): Remove the first occurrence of the mentioned value.

Miscellaneous

count(value): Return the total number of occurrences of the given value.

index(e, start, end): Search the given element from start to finish and return the index of the first occurrence.

rotate(n): Rotate the deque <math xmlns="http://www.w3.org/1998/Math/MathML">n</math> number of times. A positive value rotates it to the right, while a negative value rotates it to the left.

reverse(): Reverse the order of the deque.

Code:

# Import collections module:
import collections

# Initialize deque:
dq = collections.deque([4, 5, 6])

# Append to the right:
dq.append(7)
print("Append 7 to the right: ", list(dq))

# Append to the left:
dq.appendleft(3)
print("Append 3 to the left: ", list(dq))

# Append multiple values to right:
dq.extend([8, 9, 10])
print("Append 8, 9 and 10 to the right: ", list(dq))

# Append multiple values to left:
dq.extendleft([1, 2])
print("Append 2 and 1 to the left: ", list(dq))

# Insert -1 at index 5
dq.insert(5, -1)
print("Insert -1 at index 5: ", list(dq))

# Pop element from the right end:
dq.pop()
print("Remove element from the right: ", list(dq))

# Pop element from the left end:
dq.popleft()
print("Remove element from the left: ", list(dq))

# Remove -1:
dq.remove(-1)
print("Remove -1: ", list(dq))

# Count the number of times 5 occurs:
i = dq.count(5)
print("Count the number of times 5 occurs: ", i)

# Return index of '7' if found between index 4 and 6:
i = dq.index(7, 4, 6)
print("Search index of number 7 between index 4 and 6: ", i)

# Rotate the deque three times to the right:
dq.rotate(3)
print("Rotate the deque 3 times to the right: ", list(dq))

# Reverse the whole deque:
dq.reverse()
print("Reverse the deque: ", list(dq))

Time Complexity

The time complexity of all the above operations is constant i.e. O(1).

Applications of Deque Data Structure

In undo operations on software.

To store history in browsers.

For implementing both stacks and queues.

Priority Queue

The priority queue is an advanced type of the queue data structure. Instead of dequeuing the oldest element, a priority queue sorts and dequeues elements based on their priorities.

Priority queues are used to handle scheduling problems where some tasks are prioritized over others.

However, if elements with the same priority occur, they are served according to their order in the queue.

Assigning Priority Value

Generally, the value of the element itself is considered for assigning the priority. For example,

The element with the highest value is considered the highest priority element. However, in other cases, we can assume the element with the lowest value as the highest priority element.

We can also set priorities according to our needs.

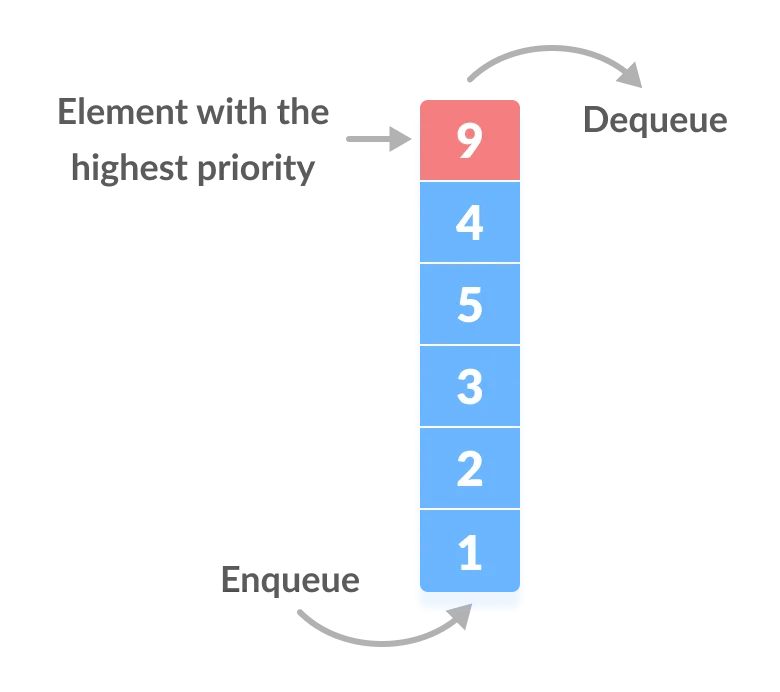
Difference between Priority Queue and Normal Queue

In a queue, the first-in-first-out rule is implemented whereas, in a priority queue, the values are removed on the basis of priority. The element with the highest priority is removed first.

The `queue.PriorityQueue` Class

Python provides a built-in implementation of the priority queue data structure.

Since the queue.PriorityQueue class needs to maintain the order of its elements, a sorting mechanism is required every time a new element is enqueued.

Python solves this by using a binary heap to implement the priority queue.

from queue import PriorityQueue

q = PriorityQueue()

q.put(4)
q.put(2)
q.put(5)
q.put(1)
q.put(3)

while not q.empty():
    next_item = q.get()
    print(next_item)

Priority-object pairs can also be inserted into the queue. This way every task can be associated with a priority.

from queue import PriorityQueue

q = PriorityQueue()

q.put((4, 'Read'))
q.put((2, 'Play'))
q.put((5, 'Write'))
q.put((1, 'Code'))
q.put((3, 'Study'))

while not q.empty():
    next_item = q.get()
    print(next_item)

Time Complexity

Operation	Worst-case Time Complexity
Insertion	O(logn)
Deletion	O(logn)

Stack

Queue

Basic Operations of Queue

Working of Queue

Enqueue Operation

Dequeue Operation

Double-Ended Queues (Deques)

Types of Deque

Insertion

Deletion

Miscellaneous

Priority Queue

The queue.PriorityQueue Class

The `queue.PriorityQueue` Class