Sorting

Sorting refers to arranging data in a particular format. Sorting algorithm specifies the way to arrange data in a particular order. Most common orders are in numerical or lexicographical order.

The importance of sorting lies in the fact that data searching can be optimized to a very high level, if data is stored in a sorted manner. Sorting is also used to represent data in more readable formats.

Following are some of the examples of sorting in real-life scenarios −

Telephone Directory − The telephone directory stores the telephone numbers of people sorted by their names, so that the names can be searched easily.

Dictionary − The dictionary stores words in an alphabetical order so that searching of any word becomes easy.

Bubble Sorting

This is the simplest sorting algorithm.
In this algorithm, we just go through each item in the collection, compare two adjacent items, and swap them if they are not in the required order.
We do this repetitively until no swaps are required.
You can consider this as one of the brute force techniques for sorting a collection.
The complexity of this algorithm is O(n²) and it is considered one of the slowest sorting algorithms.
The only reason we can use this algorithm is its simple implementation.

How Bubble Sort Works?

Starting from the“Bubble sort simply traverses the collection and compares the adjacent elements to check whether they are in the right order or not.

If they are in the proper order, then it compares the next two adjacent elements; otherwise, it swaps those two elements before moving on to the next comparison.

By doing this, it makes sure that at the end of every iteration, one element will be sorted.

For descending order, the comparison changes from < to >, but the algorithm remains the same.”

Code:

def bubble_sort(list):
    sorted=False
    while(sorted==False):
          sorted=True
          for i in range(1,len(list)):
               if(list[i]<list[i-1]):
                    list.insert(i-1,list.pop(i))
                    sorted=False
    return list

arr=[17,12,29,21,5,7]
arr=bubble_sort(arr)
print(arr)

Exercise:

Sort in the descending order.

Also sort an array of words.

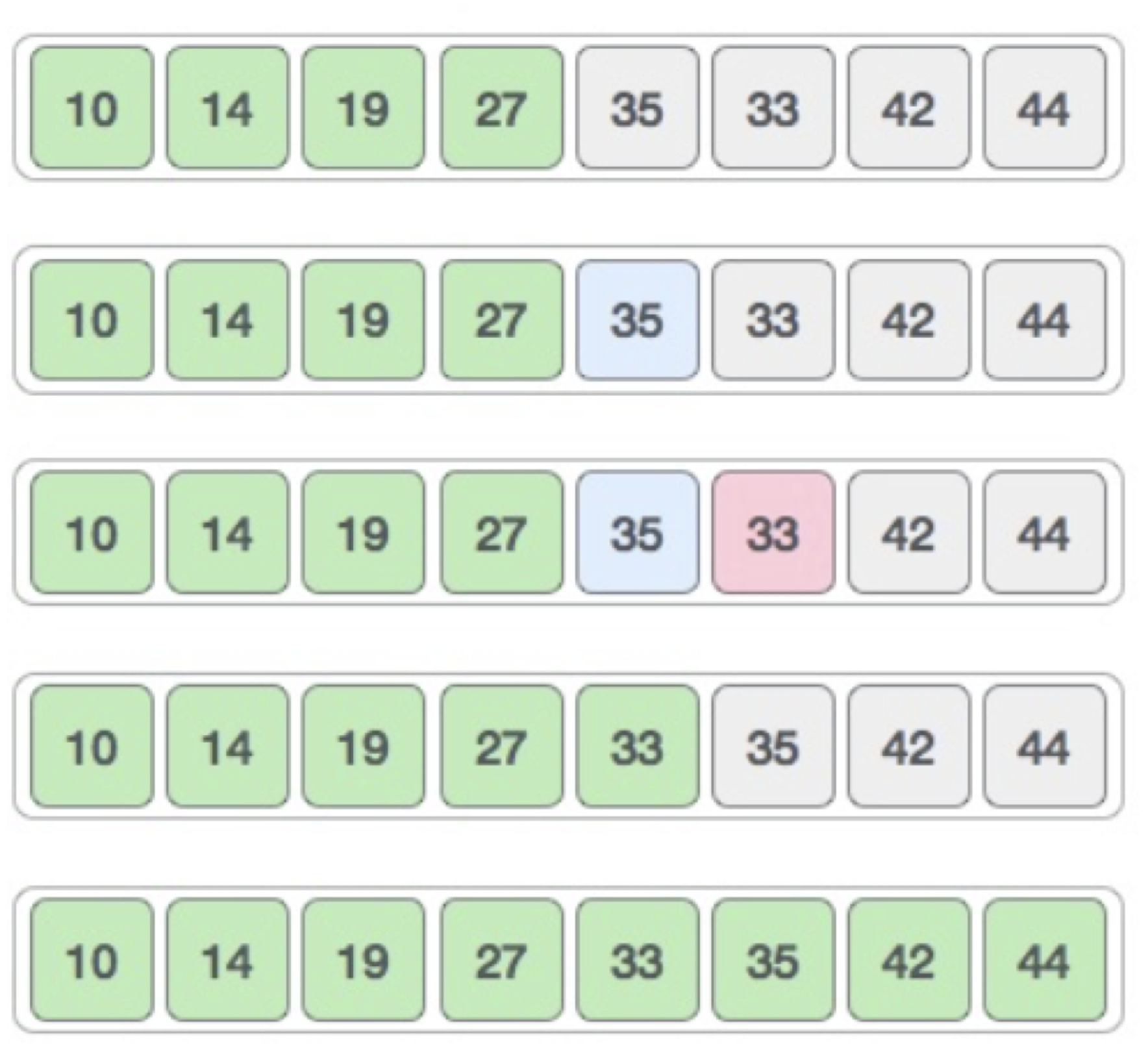
Selection Sort

Selection sort is a simple sorting algorithm.

This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.

The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right.

This algorithm is not suitable for large data sets as its average and worst case complexities are of Ο(n²), where n is the number of items.

Code:

def selectionSort(array):
    size = len(array)

    for it in range(size - 1):
        min_index = it

        for s in range(it + 1, size):
            if array[s] < array[min_index]:
                min_index = s
        
        array[it], array[min_index] = array[min_index], array[it]
    return array

array = [14,33,27,10,35,19,42,44]
print(selectionSort(array))

Quick Sort

Quick sort uses the principle of divide and conquer

It also takes O(n log n) to do its job, but in the extreme worst case, it can take O(n²) to sort n elements (which is very rare).

We can do this in place, so the memory used in quick sort is less.

How the algorithm works?

It chooses an element called the pivot element

It divides the input collection into two sub-collections based on the pivot element

The division happens in a way that all elements in the left sub-collection are smaller than the pivot element, and all elements in the right sub-collection are larger than the pivot element

Now, the pivot element is at its proper place, so we freeze it

Repeat step 1 to step 4 until the sub-collection size becomes 0 or 1

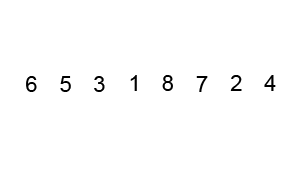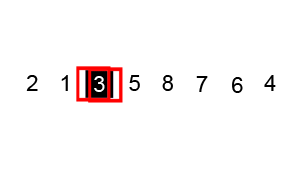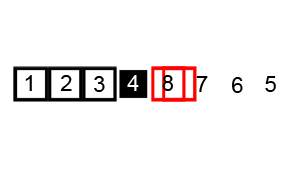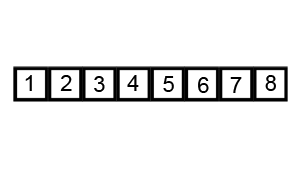
Choosing a Pivot

There is no hard and fast rule for choosing the pivot element. Here are a few ways:

Choose the first element as the pivot element

Choose the last element as the pivot element

Choose the middle element as the pivot element

Choose a random element as the pivot element

Code:

def partition(intArray, low, high):
    pi = intArray[high]
    i = low - 1
    
    for j in range(low, high):
        if intArray[j] <= pi:
            i += 1
            intArray[i], intArray[j] = intArray[j], intArray[i]
    
    intArray[i+1], intArray[high] = intArray[high], intArray[i+1]
    
    return i+1

def quick_sort(intArray, low, high):
    if low < high:
        pi = partition(intArray, low, high)
        
        quick_sort(intArray, low, pi - 1)
        quick_sort(intArray, pi + 1, high)

intArray = [64, 25, 12, 22, 11]
quick_sort(intArray, 0, len(intArray) - 1)
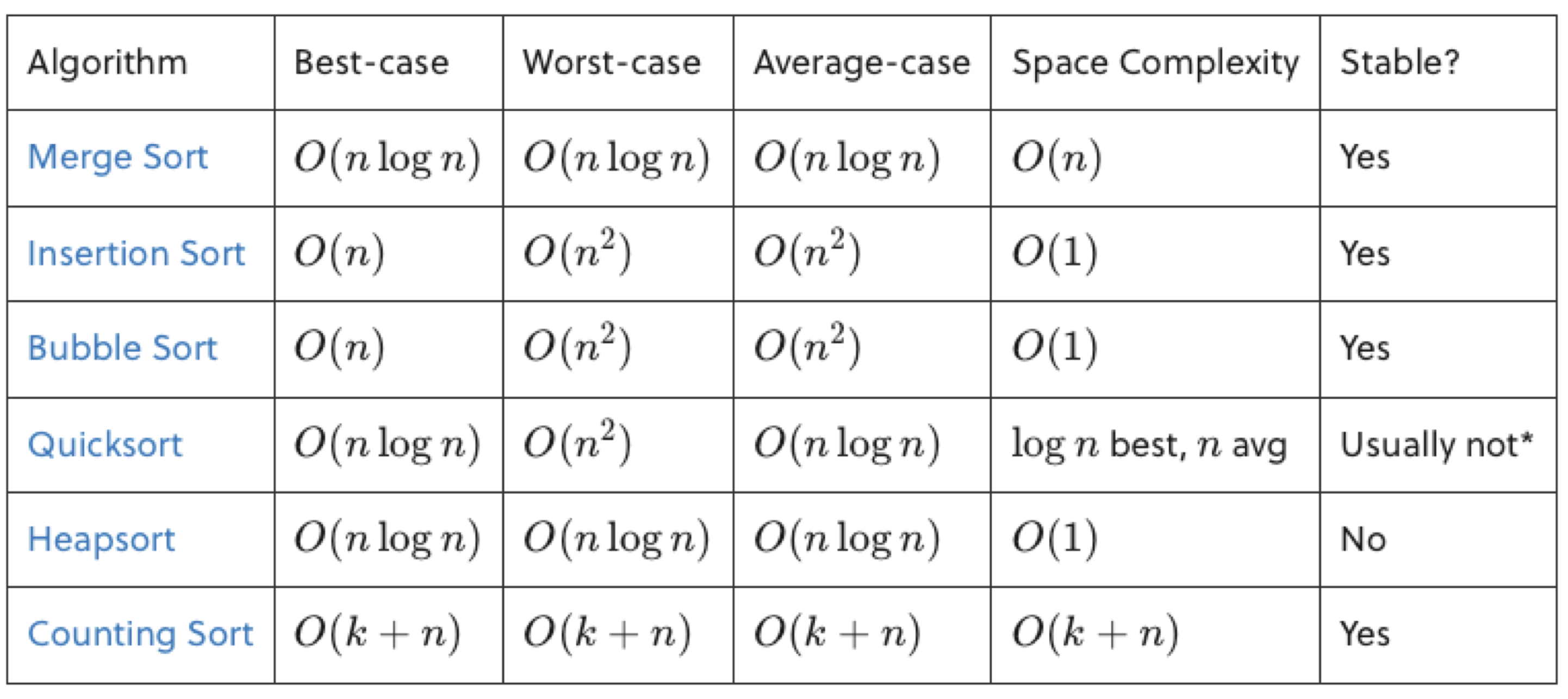
print(intArray)

Complexity of each Algorithm

Object Sort

We can sort objects of a class in an array.

Code:

class Person:
    def __init__(self, name, age):
        self.name = name
        self.age = age
    
    def get_name(self):
        return self.name
    
    def get_age(self):
        return self.age

def obj_sort():
    people = [
        Person("Kyle", 24),
        Person("Karen", 22),
        Person("Alison", 24),
        Person("Joe", 20)
    ]
    
    people.sort(key=lambda p: (p.get_age(), p.get_name()))
    
    for person in people:
        print(f"{person.get_name()}: {person.get_age()}")

obj_sort()

Search Algorithms

Linear Search

Linear search is a very simple search algorithm. In this type of search, a sequential search is made over all items one by one.

Every item is checked and if a match is found then that particular item is returned, otherwise the search continues till the end of the data collection.

Time complexity of Linear search algorithm is O(n)

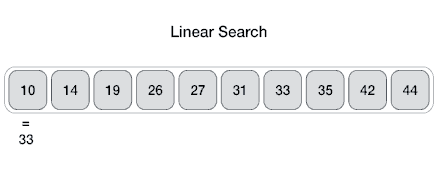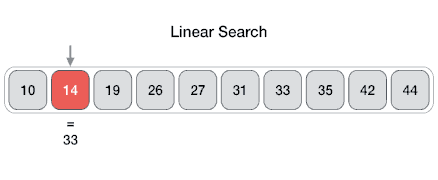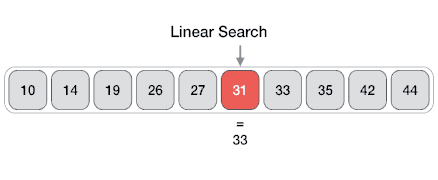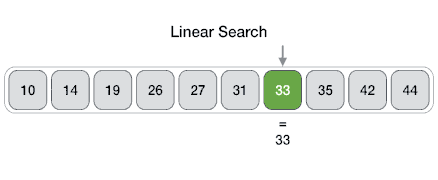
Code:

def linear_search(arr, x):
    n = len(arr)
    for i in range(n):
        if arr[i] == x:
            return i
    return -1


arr = [10, 14, 19, 26, 27, 31, 33, 35, 42, 44]
x = 33
result = linear_search(arr, x)
if result != -1:
    print(f"Element found at index {result}")
else:
    print("Element not found")

Binary Search

Binary search is a fast search algorithm with run-time complexity of Ο(log n).

This search algorithm works on the principle of divide and conquer.

For this algorithm to work properly, the data collection should be in the sorted form.

A binary search algorithm works on the idea of neglecting half of the list on every iteration.

It keeps on splitting the list until it finds the value it is looking for in a given list.

A binary search algorithm is a quick upgrade to a simple linear search algorithm.

Code:

def binary_search(array, num):
    beg = 0
    end = len(array) - 1

    while beg <= end:
        mid = (beg + end) // 2

        if array[mid] < num:
            beg = mid + 1
        elif array[mid] > num:
            end = mid - 1
        elif array[mid] == num:
            return mid
    
    # Return an index -1 if the number in the sorted array does not exist
    return -1


array = [1, 5, 7, 8, 13, 19, 20, 23, 29]
num = 23
result = binary_search(array, num)
if result != -1:
    print(f"Element found at index {result}")
else:
    print("Element not found")

Interpolation Search

Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in a sorted form and equally distributed.

Binary search has a huge advantage of time complexity over linear search. Linear search has worst-case complexity of Ο(n) whereas binary search has Ο(log n).

There are cases where the location of target data may be known in advance.

For example, in case of a telephone directory, if we want to search the telephone number of Morphius. Here, linear search and even binary search will seem slow as we can directly jump to memory space where the names start from 'M' are stored.

Similar to binary search, interpolation search can only work on a sorted array. It places a probe in a calculated position on each iteration. If the probe is right on the item we are looking for, the position will be returned; otherwise, the search space will be limited to either the right or the left side of the probe.

The probe position calculation is the only difference between binary search and interpolation search.

In binary search, the probe position is always the middlemost item of the remaining search space.

In contrary, interpolation search computes the probe position based on this formula:

Example:

Code:

def interpolation_search(data, item):
    high_end = len(data) - 1
    low_end = 0

    while item >= data[low_end] and item <= data[high_end] and low_end <= high_end:
        probe = low_end + (high_end - low_end) * (item - data[low_end]) // (data[high_end] - data[low_end])

        if high_end == low_end:
            if data[low_end] == item:
                return low_end
            else:
                return -1

        if data[probe] == item:
            return probe

        if data[probe] < item:
            low_end = probe + 1
        else:
            high_end = probe - 1
    
    return -1


data = [13, 21, 34, 55, 69, 73, 84, 101]
item = 84
result = interpolation_search(data, item)
if result != -1:
    print(f"Element found at index {result}")
else:
    print("Element not found")