What is the Monte Carlo Simulation?

A Monte Carlo method is a technique that uses random numbers and probability to solve complex problems.

The Monte Carlo simulation, or probability simulation, is a technique used to understand the impact of risk and uncertainty in financial sectors, project management, costs, and other forecasting machine learning models.

Risk analysis is part of almost every decision we make, as we constantly face uncertainty, ambiguity, and variability in our lives. Moreover, even though we have unprecedented access to information, we cannot accurately predict the future.

The Monte Carlo simulation allows us to see all the possible outcomes of our decisions and assess risk impact, in consequence allowing better decision making under uncertainty.

Applications of Monte Carlo Simulation

Finance.
Project Management.
Energy.
Manufacturing.
Engineering.
Research and Development.
Insurance.
Oil and Gas.
Transportation.
Environment.
And others.

Example: Flipping a coin

The probability of head for a fair coin is 1/2. However, is there any way we can prove it experimentally?

In this example, we are going to use the Monte-Carlo method to simulate the coin-flipping iteratively 5000 times to find out why the probability of a head or tail is always 1/2.

If we repeat this coin flipping many, many more times, then we can achieve higher accuracy on an exact answer for our probability value.

Code:

# 1. Coin Flip Example
#Import required libraries :

import random
import numpy as np
import matplotlib.pyplot as plt

#Coin flip function :

#0 --> Heads
#1 --> Tails

def coin_flip():
    return random.randint(0,1) 

#Monte Carlo Simulation :

#Empty list to store the probability values.
list1 = []


def monte_carlo(n):
    results = 0
    for i in range(n):
        flip_result = coin_flip()
        results = results + flip_result
        
        #Calculating probability value :
        prob_value = results/(i+1)
        
        #Append the probability values to the list :
        list1.append(prob_value)

        #Plot the results :
        plt.axhline(y=0.5, color='r', linestyle='-')
        plt.xlabel("Iterations")
        plt.ylabel("Probability")
        plt.plot(list1)
       
    return results/n
  
#Calling the function :

answer = monte_carlo(5000)
print("Final value :",answer)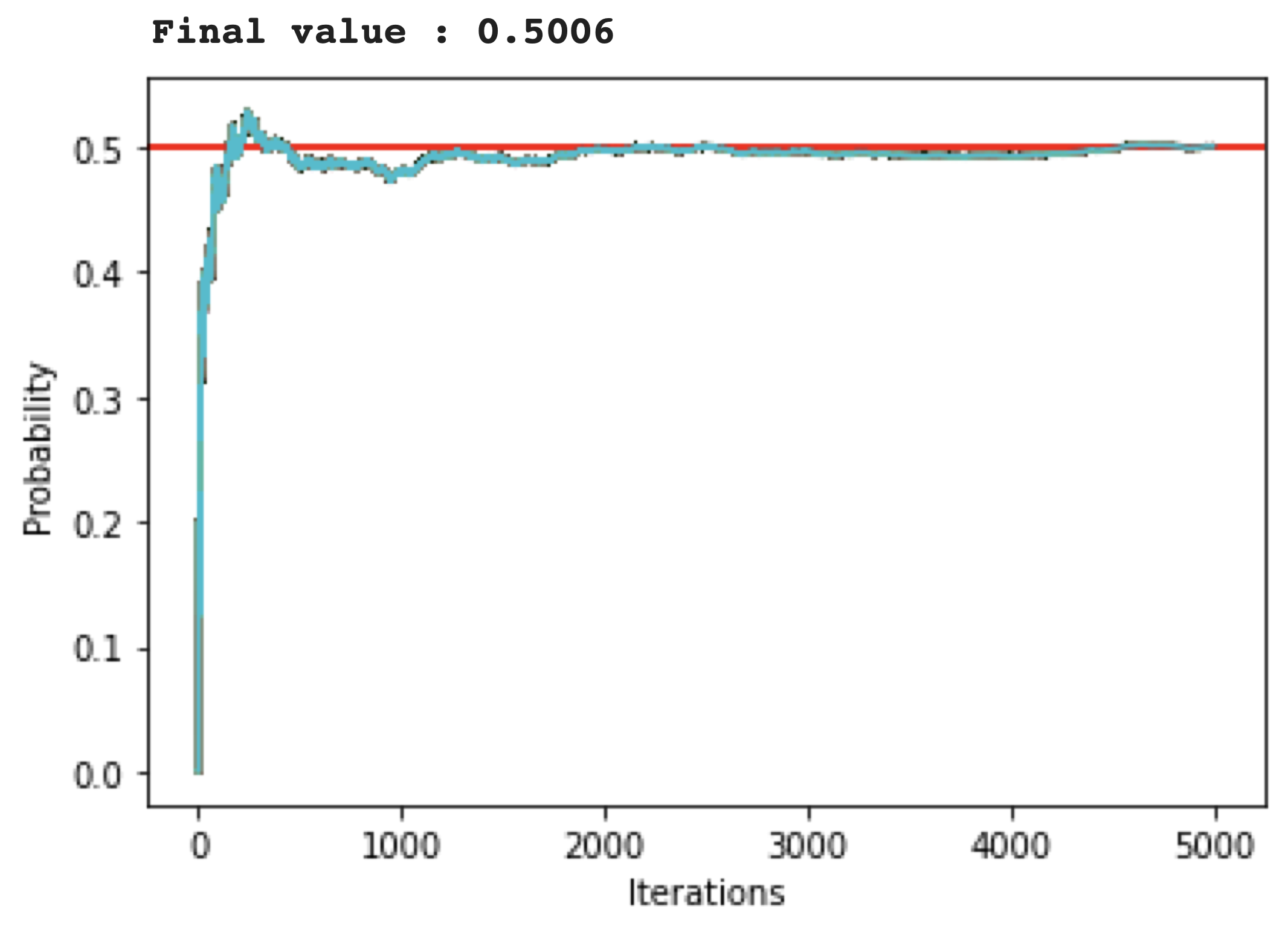

Example:- Monty Hall Problem

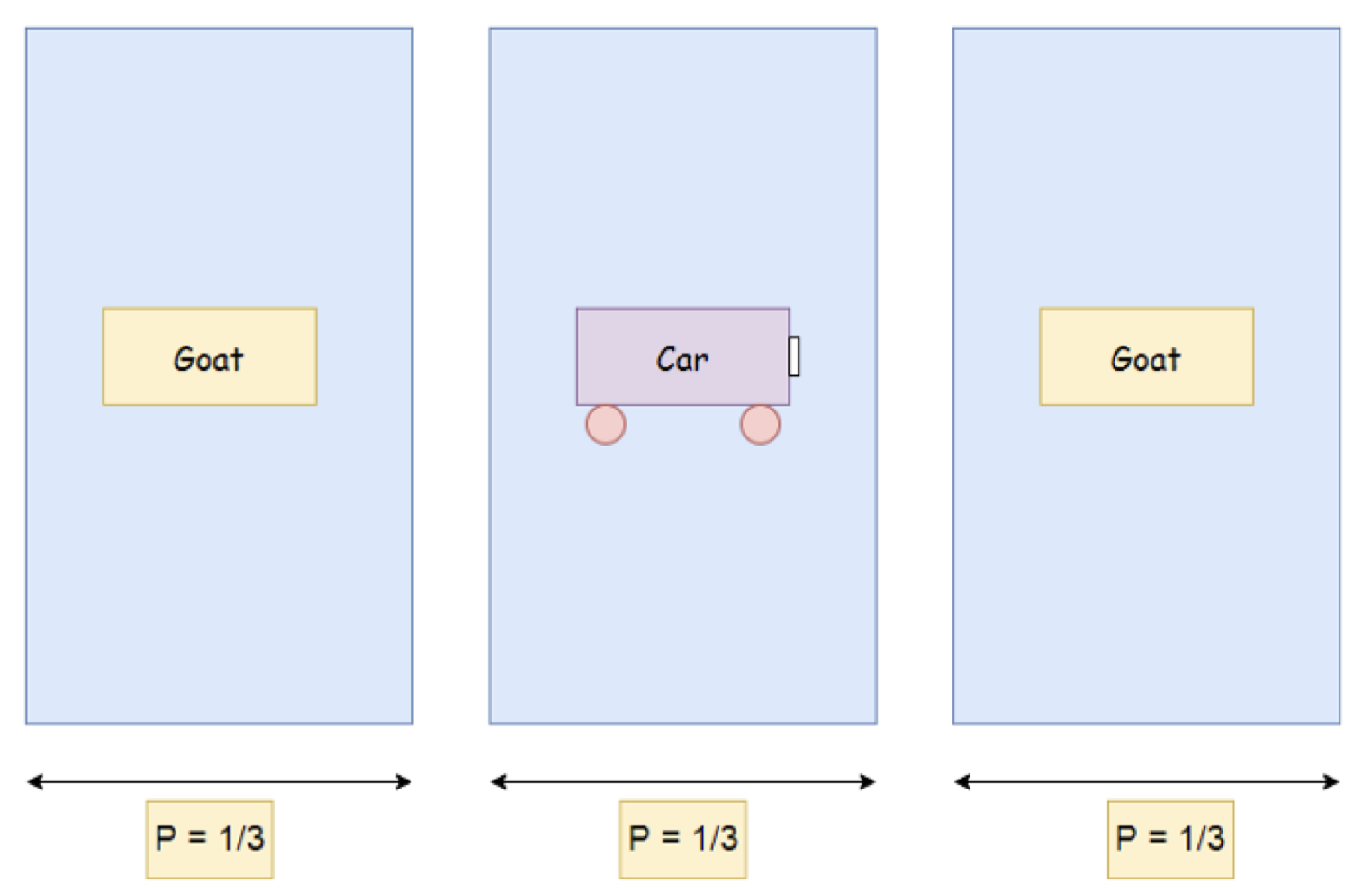
Suppose you are on a game show, and you have the choice of picking one of three doors: Behind one door is a car; behind the other doors, goats.

You pick a door, let’s say door 1, and the host, who knows what’s behind the doors, opens another door, say door 3, which has a goat. The host then asks you: do you want to stick with your choice or choose another door?

Is it to your advantage to switch your choice of door?

Based on probability, it turns out it is to our advantage to switch the doors. Let’s find out how:

Initially, for all three gates, the probability (P) of getting the car is the same (P = 1/3).

Now assume that the contestant chooses door 1. Next, the host opens the third door, which has a goat. Next, the host asks the contestant if he/she wants to switch the doors?

We will see why it is more advantageous to switch the door:

We can see that after the host opens door 3, the probability of the last two doors of having a car increases to 2/3. Now we know that the third door has a goat, the probability of the second door having a car increases to 2/3.

Hence, it is more advantageous to switch the doors.

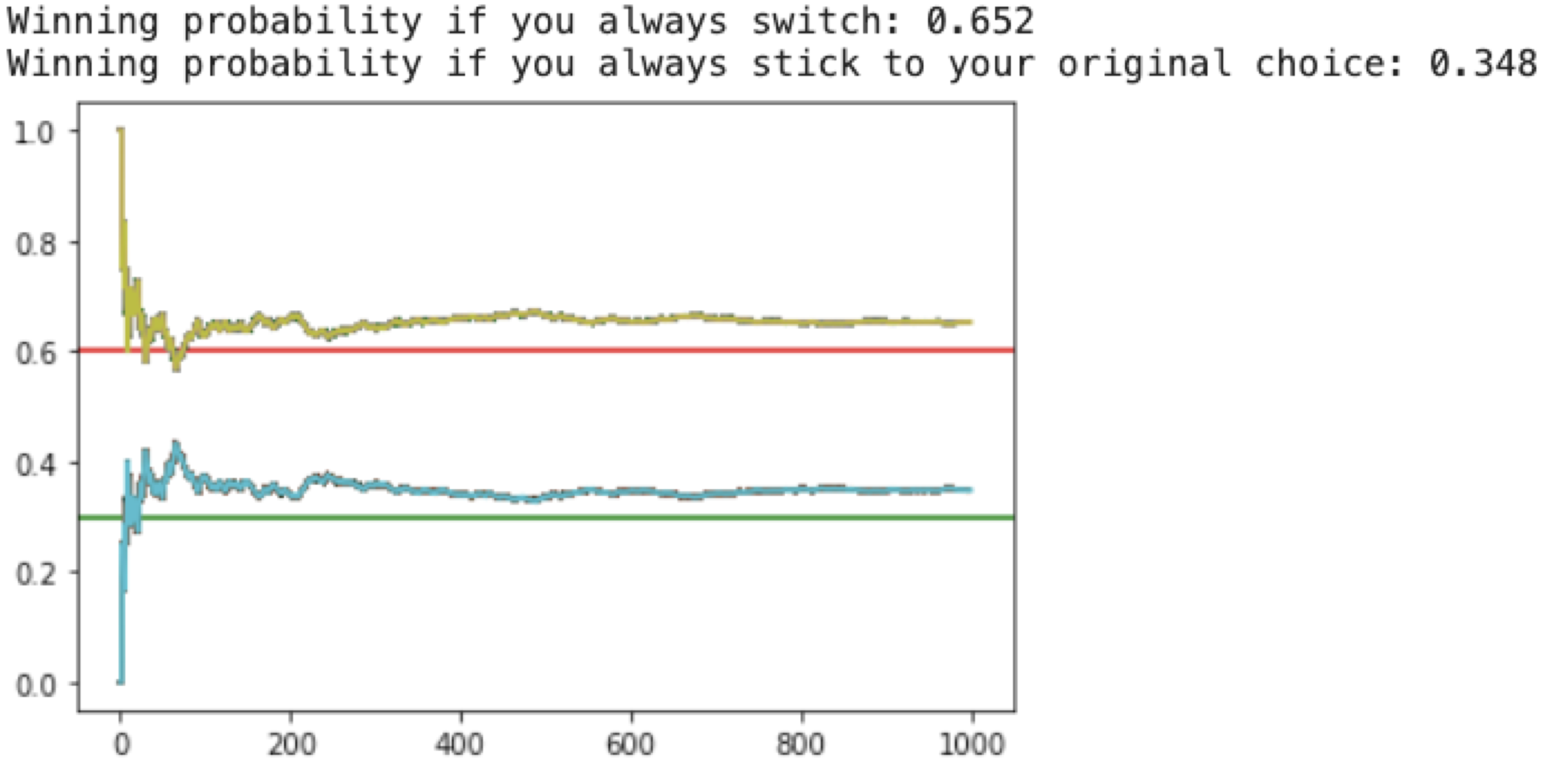
Now we are going to use the Monte Carlo Method to perform this test case many times and find out it’s probabilities in an experimental way.

Code:

# 3. Monty Hall Problem
#Import required libraries :
import random
import matplotlib.pyplot as plt

#We are going with 3 doors :
#1 - Car
#2 - Goats
doors = ["goat","goat","car"]

#Empty lists to store probability values :
switch_win_probability = []
stick_win_probability = []

plt.axhline(y=0.6, color='r', linestyle='-')
plt.axhline(y=0.3, color='g', linestyle='-')

#Monte_Carlo Simulation :
def monte_carlo(n):
    
    #Calculating switch and stick wins :
    switch_wins = 0
    stick_wins = 0
    
    for i in range(n):
    
        #Randomly placing the car and goats behind the three doors :
        random.shuffle(doors) 
        
        #Contestant's choice :
        k = random.randrange(2)  

        #If the contestant doesn't get car :
        if doors[k] != 'car': 
            switch_wins += 1
            
        #If the contestant got car :
        else: 
            stick_wins += 1

        #Updating the list values :
        switch_win_probability.append(switch_wins/(i+1))
        stick_win_probability.append(stick_wins/(i+1))
        
        #Plotting the data :
        plt.plot(switch_win_probability)
        plt.plot(stick_win_probability)
        
    #Print the probability values :
    print('Winning probability if you always switch:',switch_win_probability[-1])
    print('Winning probability if you always stick to your original choice:', stick_win_probability[-1])


#Calling the function :
monte_carlo(1000)